Half Adder
With the help of half adder, we can design circuits that are capable of performing simple addition with the help of logic gates.
Let us first take a look at the addition of single bits.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
These are the least possible single-bit combinations. But the result for 1+1 is 10. Though this problem can be solved with the help of an EXOR Gate, if you do care about the output, the sum result must be re-written as a 2-bit output.
Thus the above equations can be written as
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Here the output ‘1’of ‘10’ becomes the carry-out. The result is shown in a truth-table below. ‘SUM’ is the normal output and ‘CARRY’ is the carry-out.
INPUTS OUTPUTS
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
From the equation it is clear that this 1-bit adder can be easily implemented with the help of EXOR Gate for the output ‘SUM’ and an AND Gate for the carry. Take a look at the implementation below.
- Half Adder Circuit
For complex addition, there may be cases when you have to add two 8-bit bytes together. This can be done only with the help of full-adder logic.
Full Adder
This type of adder is a little more difficult to implement than a half-adder. The main difference between a half-adder and a full-adder is that the full-adder has three inputs and two outputs. The first two inputs are A and B and the third input is an input carry designated as CIN. When a full adder logic is designed we will be able to string eight of them together to create a byte-wide adder and cascade the carry bit from one adder to the next.
The output carry is designated as COUT and the normal output is designated as S. Take a look at the truth-table.
INPUTS OUTPUTS
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
From the above truth-table, the full adder logic can be implemented. We can see that the output S is an EXOR between the input A and the half-adder SUM output with B and CIN inputs. We must also note that the COUT will only be true if any of the two inputs out of the three are HIGH.
Thus, we can implement a full adder circuit with the help of two half adder circuits. The first will half adder will be used to add A and B to produce a partial Sum. The second half adder logic can be used to add CIN to the Sum produced by the first half adder to get the final S output. If any of the half adder logic produces a carry, there will be an output carry. Thus, COUT will be an OR function of the half-adder Carry outputs. Take a look at the implementation of the full adder circuit shown below.
- Full Adder Circuit
Though the implementation of larger logic diagrams is possible with the above full adder logic a simpler symbol is mostly used to represent the operation. Given below is a simpler schematic representation of a one-bit full adder.
- Single-bit Full Adder
With this type of symbol, we can add two bits together taking a carry from the next lower order of magnitude, and sending a carry to the next higher order of magnitude. In a computer, for a multi-bit operation, each bit must be represented by a full adder and must be added simultaneously. Thus, to add two 8-bit numbers, you will need 8 full adders which can be formed by cascading two of the 4-bit blocks. The addition of two 4-bit numbers is shown below.



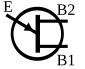
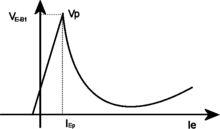
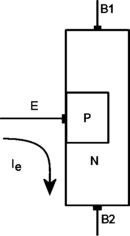
 (the "intrinsic stand-off ratio"). The 2N2646 model is the most commonly used version of the UJT.
(the "intrinsic stand-off ratio"). The 2N2646 model is the most commonly used version of the UJT.